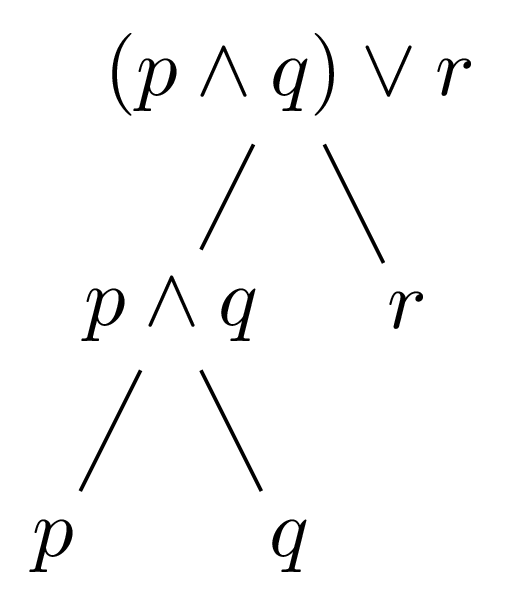Normal forms
Jump to Section
Disjunctive Normal Form (DNF)
| p | q | r | \(f\) | Clause Conjunction |
|---|---|---|---|---|
| F | F | F | T | \(\neg p \wedge \neg q \vee \neg r\) |
| F | F | T | F | |
| F | T | F | T | \(\neg p \wedge \neg q \wedge r\) |
| F | T | T | T | \(\neg p \wedge q \wedge r\) |
| T | F | F | F | |
| T | F | T | F | |
| T | T | F | T | \(p \wedge q \wedge \neg r\) |
| T | T | T | T | \(p \wedge q \wedge r\) |
- Take all of the true statements in the table and write a clause for them
- Concatenate all of the true clauses together with a disjunction statement \(\vee\)
- \(\neg f \Leftrightarrow (\neg p \wedge \neg q \wedge \neg r) \vee (\neg p \wedge q \wedge \neg r) \vee ( \neg p \wedge q \wedge r) \vee (p \wedge q \wedge r) \vee (p \wedge q \wedge \neg r) \vee (p \wedge q \wedge r)\)
Conjunctive Normal Form (CNF)
- Negate the DNF form
- \(\neg (\neg f) \Leftrightarrow f\)
- Use demorgans law to distribute
Expression Trees
A binary tree representation of the logical expression