Mock Exam Questions

Jump to Section

Question 1 and 2 seem to reference this article: 8086-8088

Q1

If a physical branch target address is 5A230 when CS = 5200, what will it be if the CS = 7800 ?

We need to find the offset, where offset + CS(shifted 4 bits) = physical branch target address. CS(C segment register)
Offset = Physical branch target address - CS
Offset = 5A230 - 52000 = 8230 (hex)

The offset is then used to find the physical branch target adress.

78000 + 8230 = 80230 = physical branch target address

Q2

Given that the EA of a data is 2359 and DS = 490B, what is the PA of data?

EA (effective Address), DS (D segment register), PA(Physical Address).

Physical address is given by EA + DS(shifted 4 bits).

DS = 490B0 (hex)
EA = 2359 (hex)
PA = 490B0 + 2359 = 4B409

Q3

Assuming, W, X, Y and Z as memory addresses. Write a program using any machine sequence that will carry out the following: Z ← W + (Z-X).

    .globl main
    .text

main:
    lw $t1, Z #load z into temporary register 1
    lw $t2, X #load x into temporary register 2
    sub $s1, $t1, $t2 #s1 <- t1-t2
    lw $t1, W #load w into temporary register 1
    add $s1, $t1, $s1 #s1 <- t1
    sw $s1, Z # stores s1 into Z

    li $v0, 1 #prints z
    lw $a0, Z
    syscall

    li $v0, 10 #exits
    syscall


.data
Z: .word  12 #arbitrary value
X: .word 10 #arbitrary value
W: .word 5 #arbitrary value

Downloadable solution prints 7

Q4

Assume that the code below is run on a machine with a 2 GHz clock that requires the following number of cycles for each instruction: add, addi, sll, sra take 4cc each, lw takes 5cc, bne, beq take 3cc each. How many seconds will it take to execute this code. The values of registers are $4=0x20, $5= 0x20, $6= 0x30, $7= 0x10.

    .globl  main
    .text

main:
    sra $6, $6, 2   # changes original value of 0x30 / 2^2  = 0xC
    sll $7, $7, 2 # original value = 0x10, 0x10 * 2^2 = 0x40
    add $8, $0, $0 # sets register 8 to 0
L2: add $12, $4, $8 #marks L2, $12 <- 0x20 + $8, $8 is iterator
    lw  $12, 0($12) # $12 = memory at address of ($12) on stack
    add $9, $0, $0 # $9 = 0;
L1: add $11, $5, $9 #marks L1, $11 = 0x20 + $9, $9 is iterator
    lw  $11, 0($11) #$11 = memory at address of ($11) on stack
    addi $9, $9, 4 #$9 = $9 + 4
    bne $9, $7, L1 # goes to L1 if $9 != $7  0x0 + 0x4 * 0x10 = 0x40 = $9 loop executes 0x10 times
    addi $8, $8, 4 # $8 = $8 + 4
    beq $8, $6, L2 # goes to L2 if $8 == $6 exits before  $8 can equal $6

Instruction definitions

sra (shift right arithmetic) (sra destination, origin, shift(in bits)) rounds down
sll (shift left logical) (sll destination, origin, shift)
bne (bne r1, r2, branch address) goes to branch address if r1 != r2
beq (beq, r1, r2, branch address) goest to branch address if r1 == r2

Calculate number of clock cycles

Before loops

sra 4cc
sll 4cc
add 4cc
total = 12cc

L2

add 4cc
lw 5cc
add 4cc
L1 clocks
addi 4cc
beq 3cc
total = (20cc + L1 clocks)*1 loop

L3

add 4cc
lw 5cc
addi 4ccc
bne 3cc
total = (16cc * 16 loops) = 256 clocks

Total clocks

12cc + 20cc + 256cc = 288cc

Calculate time

288cc/(2*10^9cc/s) = 1.44 * 10^-7 seconds

Q5

X[i] = A[B[i]] + C[i+4]

starting address of A in $1
starting address of B in $2
starting address of C in $3
starting address of X in $4
i value in register $5

Q5 Solution download

.globl main
.text

main:
    sll     $s4, $5, 2          # multiplies i * 4 to conform to address form
    add     $t2, $2, $s4        # gets address of B[i] offsets address of B by i
    lw      $t3, ($t2)          # sets t3 to value at address t3 = B[i]

    sll     $t1, $t3, 2         # sets t1 to t3 * 4 to conform to address form
    add     $t2, $1, $t1        # offsets addres value in $1 by $t1 A[B[i]]
    lw      $s1, ($t2)          # sets t3 to value at address $t2 t3 = A[B[i]]

    addi    $t1, $5, 4          # offsets i by 4  = i+4
    sll     $t1, $5, 2          # multiplies i*4 to conform to address form
    add     $t2, $3, $t1        # offsets C address by i+4
    lw      $s2, ($t2)          # s2 = C[i+4]

    add     $t1, $s1, $s2       # adds A[B[i]] + C[i+4]
    add     $s3, $4, $s4        # offsets address of X by i
    sw      $t1, ($s3)          # stores $t1 to address of ($s3)

Q6

The memory units that follow are specified by the number of words times the number of bits per word. How many address lines and input/output data lines are needed in each case? (a) 8K X 16 (b) 2G X 8 (c) 16M X 32 (d) 256K X 64

Part A

Number of words = 8K
Number of bits per word = 16
log base 2 of words = address lines
2^3 * 2^10 = 2^13 = 13 address lines
I/O lines = address lines + bits per word
13 + 16 = 29 I/O lines

Part B

2^1 * 2^30 = 2G
Address lines = 31
I/O lines = 31 + 8 = 39
39 I/O lines

Part C

2^4 * 2^20 = 16M
Address lines = 24
I/O lines = 24 + 32 = 56
56 I/O lines

Part D

2^8 * 2^10 = 256K
Address lines = 18
I/O lines = 18 + 64
82 I/O lines

Q7

Find the number of bytes that can be stored in the memories: (a) 8K X 16 (b) 2G X 8 (c) 16M X 32 (d) 256K X 64

Part A

8 bits per byte
8K words
16 bits per word
number of bits = 8K*16 = 2^13 * 2^4 = 2^17
number of bytes = 2^17/2^3 = 2^14 = 16K bytes

Part B

Number of bits = 2G*8 = 2^31*2^3
Number of bytes = 2^31*2^3/2^3 = 2^31 = 2G bytes

Part C

Number of bytes = 16M * 32 / 2^3 = 2^24 * 32 /2^3 = 2^26 = 64M bytes

Part D

Number of bytes = 256K*64/2^3 = 2^18 * 64 /2^3 = 2^24 /2^3 = 2^21 = 2M bytes

TODO Q8

How many 128 x 8 memory chips are needed to provide a memory capacity of 4096 x 16?

4096*16 / 128*8 = 64

Q9

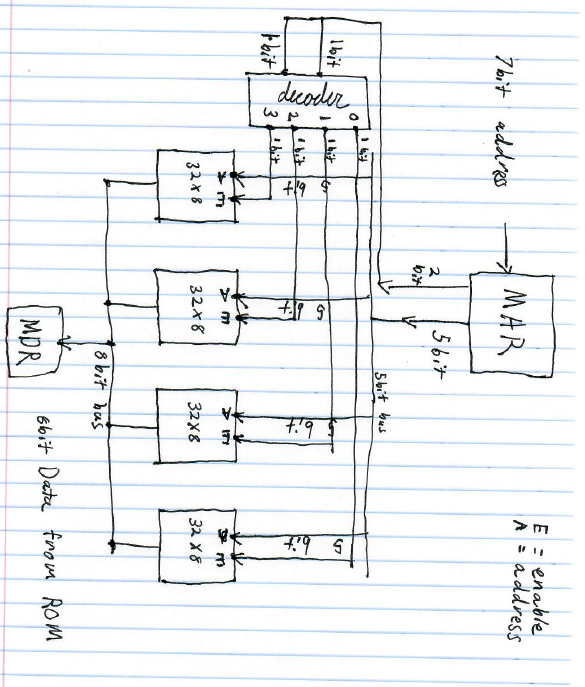
Given a 32 x 8 ROM chip with an enable input, show the external connections necessary to construct a 128 x 8 ROM with four chips and a decoder. Useful Video

2^5 = 32
5 address lines for each ROM
128/32 = 4 chips
4 outputs on decoder (connected to enable inputs)
2^2 = 4
2 address lines for the decoder
5 + 2 = 7 total lines for complete address

Q10

Assume we have 8GB of word addressable memory with a word size of 64 bits and each refill line of memory stores 16 words. We have a direct-mapped cache with 1024 refill lines. Answer the following questions. More examples

What is the address format for the cache
If we changed the cache to a 2-way set associative cache, how does the format change?
If we changed the cache to a fully associative cache, how does the format change?

Solution

Part 1

8GB = 8*2^30 bytes
64 bit word = 8 byte word
8GB / 8 byte word = 1GW (gigaword)
1G = 2^30
30 bits for line addresses
16 words per line = 2^4
4 bits for word number on line
address format (for MM) = [30-4 bit line address][4 bit word address]
1024 refill lines = 2^10
10 bits for line number
26-10 bits for tag
[tag][line number][word number]
16-10-4 = cache memory format

Part 2

2 way set associate cache
divide refill lines by 2
1024/2 = 512 = 2^9
26-9 = tag
17-9-4 = 2 way set cache memory format

Part 3

fully associative cache
1 refill line = 2^0
26-0 = tag
26-0-4 = fully associate cache

Hard Drive Sample question

This is a writeup of question 1 from here.

Consider a disk pack with the following specifications 16 surfaces, 128 tracks per surface, 256 sectors per track, 512 bytes per sector

Capacity of Disk Space

Use the formula Capacity of Disk Space. 16 surfaces * 128 tracks/surface * 256 sectors/track * 512 bytes per sector = $2^{28}$ bytes = 256 MB

Useful formulas and references