11/22/2021

Before reading this Daily PL, please re-read the one from Friday, 11/19/2021. The content has been updated since it was originally published to reflect certain errors with the “better” Integer grammar we developed in class. Thanks, especially, to Jeroen for making sure that I got the grammar correct!

Making Meaning

In an earlier part of the class we talked about how to describe the dynamic semantics of a program. We worked closely with operational semantics but saw other examples, too (axiomatic and denotational). Although we said that what we are studying in this module is the syntax of a language and not its semantics, a language may have static semantics that the compiler can check during syntax analysis. Syntax analysis is done using a tool known as the parser.

Remember that syntax and syntax analysis is only concerned with valid programs. If the program, considered as a string of letters of the language’s alphabet, can be derived from the language grammar’s start symbol, then the program is valid. We all agreed that was the limit of what a syntax analyzer could determine.

One form of output of a parser is a parse tree. It is possible to apply “decoration” to the parse tree in order to verify certain extra-syntactic properties of a program at the time that it is being parsed. These properties are known as a language’s static semantics. More formally, Sebesta defines static semantics as the rules for a valid program in a particular language that are difficult (or impossible!) to encode in a grammar. Checking static semantics early in the compilation process is incredibly helpful for programmers as they write their code and allows the stages of the compilation process after syntax analysis to make more sophisticated assumptions about a program’s validity.

One example of static semantics of a programming language has to do with its type system. Checking a program for type safety is possible at the time of syntax analysis using an attribute grammar. An attribute grammar is an extension of a CFG that adds (semantic) information to its terminals and nonterminals.​ This information is known as attributes. Attached to each production are attribute calculation functions. At the time the program is parsed, the attribute calculation functions are evaluated every time that the associated production is used in a derivation and the results of that invocation are stored in the nodes of the parse tree that represent terminals and nonterminals. Additionally, in an attribute grammar, each production can have a set of predicates. Predicates are simply Boolean-valued functions. When a parser attempts to use a production during parsing, it’s not just the attribute calculation functions that are invoked – the production’s predicates are too. If any of those predicates returns false, then the derivation fails. An Assignment Grammar

To start class, we looked at a snippet of an industrial-strength grammar – the one for the C programming language. The snippet we saw concerned the assignment expression:

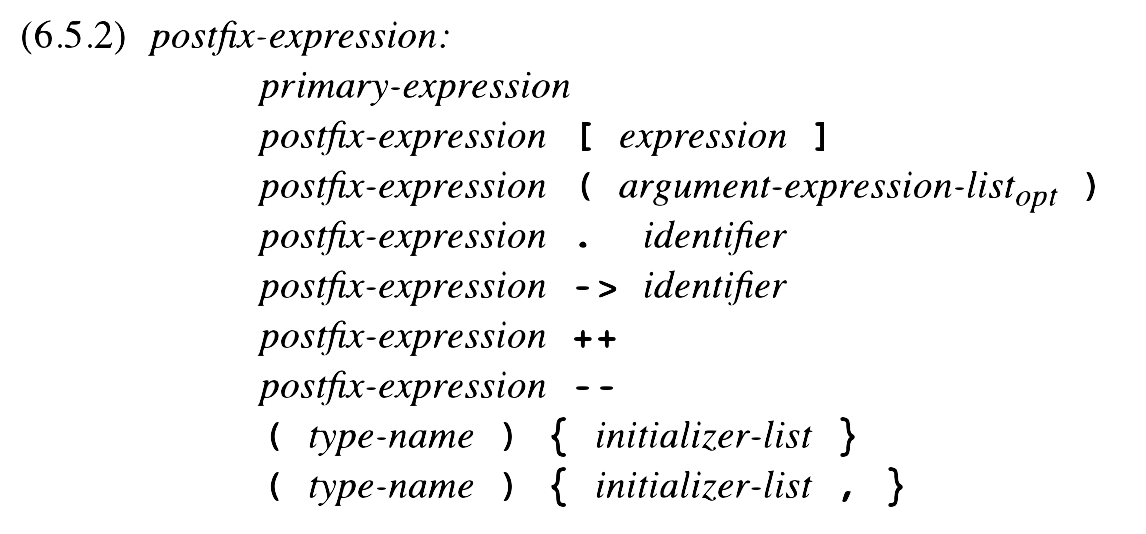
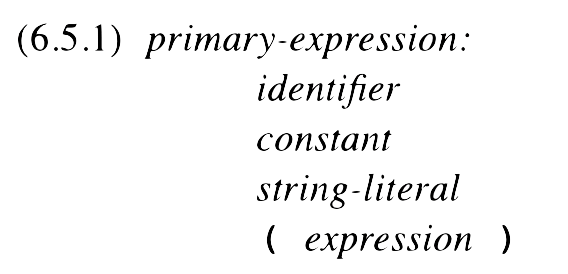
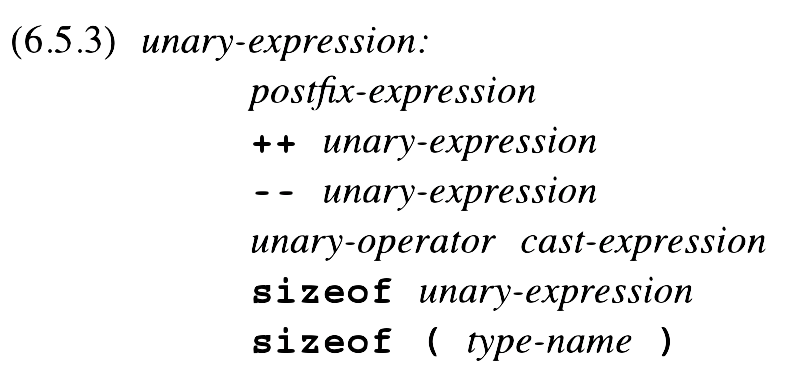
There are lots of details in the grammar for an assignment statement in C and not all of them pertain to our discussion. So, instead of using that grammar of assignment statements, we’ll use a simpler one:

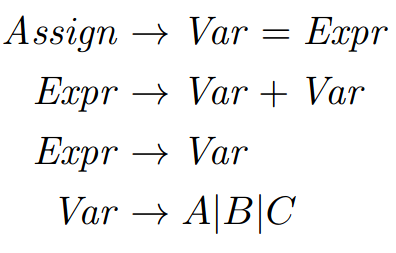
Assume that this is part of a larger grammar for a complete, statically typed programming language. In the subset of the grammar that we are going to work with, there are three terminals: A, B and C. These are variable names available for the programmer in our language. As a program in this language is parsed, the compiler builds a mapping between variables and their types (known as the symbol table), adding an entry for each new variable declaration it encounters. The compiler can “lookup” the type of a variable using its name thanks to the lookup function.

Our hypothetical language contains only two numerical types: int and real. A variable can only be assigned the result of an expression if that expression has the same type as the variable. In order to determine the type of an expression, our language adheres to the following rules:

Let’s assume that we are looking at the following program written in our hypothetical language:

int A;
real B;
A = A + B;

The declarations of the variables A and B are handled by parts of the grammar that we are not showing in our example. Again, when those declarations are parsed, an entry is made in the symbol table so that variable names can be mapped to types. Let’s derive A = A + B; using the snippet of the grammar shown above:

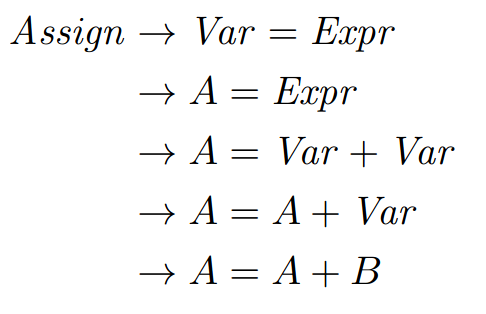
Great! The program passes the syntactic analysis so it’s valid!

Right?

This Grammar Goes To 11

Wrong. According to the language’s type rules, we can only assign to variables that have the same type as the expression being assigned. The rules say that A + B is a real (a.ii). A is declared as an int. So, even though the program parses, it is invalid!

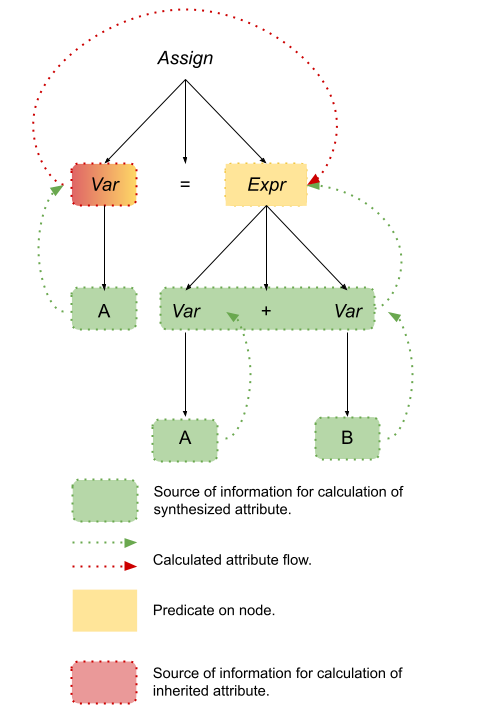
We can solve this using attribute grammars and that’s exactly what we are going to do! For our Assign grammar, we will add the following attributes to each of the terminals and nonterminals:

expected_type: The type that is expected for the expression. actual_type: The actual type of the expression.

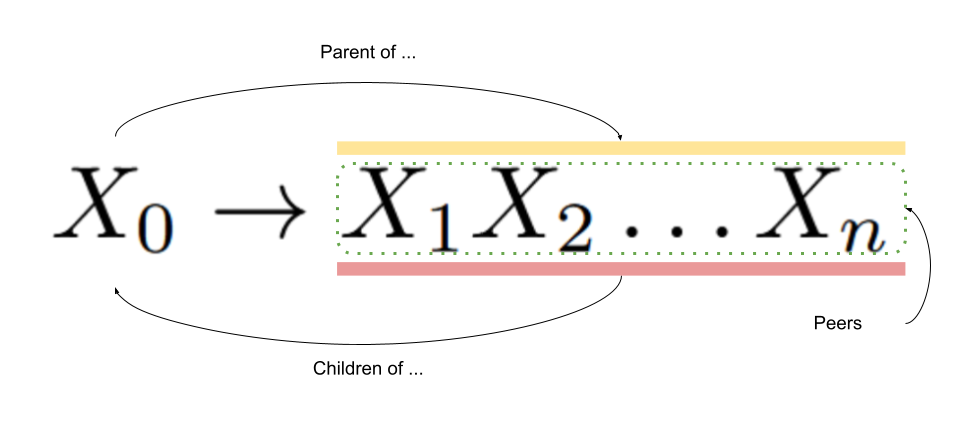
The values for the attributes are set according to functions. An attribute whose calculation function uses attribute values from only its children and peer nodes in the parse tree is known as a synthesized attribute. An attribute whose calculation function uses only attribute values from its parent nodes in the parse tree is known as an inherited attribute.

Let’s define the attribute calculation functions for the expected_type and actual_type attributes of the Assign grammar:

For this production, we can see that the expression’s expected_type attribute is defined according to the variable’s actual_type which means that it is an inherited attribute.

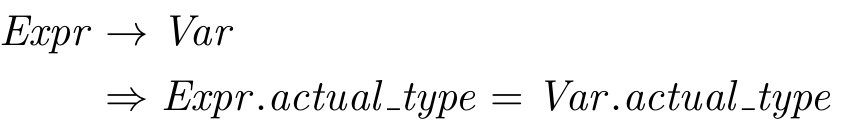
For this production, we can see that the expression’s actual_type attribute is defined according to the variable’s actual_type which means that it is a synthesized attribute.

And now for the most complicated (but not complex) attribute calculation function definition:

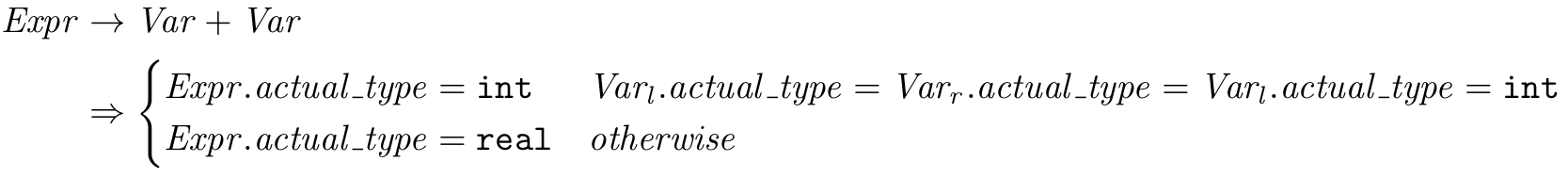
Again, we can see that the expression’s actual_type attribute is defined according to its children nodes – the actual_type of the two variables being added together – which means that it is a synthesized attribute.

If you are thinking that the attribute calculation functions are recursive, you are exactly right! And, you can probably see a problem straight ahead. So far the attribute calculation functions have relied on attributes of peer, children and parent nodes in the parse tree to already have values. Where is our base case?

Great question. There’s a third type of attribute known as an intrinsic attribute. An intrinsic attribute is one whose value is calculated according to some information outside the parse tree. In our case, the actual_type attribute of a variable is calculated according to the mapping stored in the symbol table and accessible by the lookup function that we defined above.

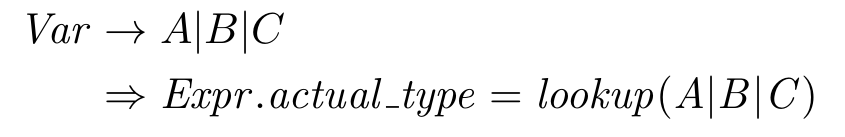
That’s all for the definition of the attribute calculation functions and is all well and good. Unfortunately, we still have not used our attributes to inform the parser when a derivation has gone off the rails by violating the type rules. We’ll define these guardrails predicate functions and show the complete attribute grammar at the same time:

The equalities after the checkmarks are the predicates. We can read them as “If the actual type of the expression is the same as the expected type of the predicate, then the derivation (parse) can continue. Otherwise, it must fail because the assignment statement being parsed violates the type rules.” Put The Icing On The Cookie

The process of calculating the attributes of a production during parsing is known as decorating the parse tree. Let’s look at the parse tree from the assignment statement A = A + B; and see how it is decorated: